Hash – Tablas de dispersión
Posted: diciembre 27th, 2008 | Author: admin | Filed under: Estructuras de datos, Software, TAD | Tags: dispersion abierta, dispersion cerrada, dispersion cuadratica, dispersion lineal, redispersion, Tablas de dispersion | Comentarios desactivados en Hash – Tablas de dispersiónEs común al crear estructuras de datos y luego trabajar sobre las mismas, tener la necesidad de realizar búsquedas en forma más frecuente que la necesidad de realizar inserciones. Por ejemplo si tenemos una lista de personas podríamos querer saber si cierta persona está ingresada, o saber información acerca de la misma. Para estos casos en que queremos realizar consultas sobre la estructura de datos puede ser útil trabajar con una estructura de datos que permita realizar búsquedas rápidas (de orden pequeño).
La estructura que vamos a ver es la Tabla de dispersión o Hash, la cual nos permite acceder a una posición dentro de la misma en orden 1, (O(1) caso promedio), realizando una cantidad fija de operaciones. De esta forma nos aseguramos de llegar a donde deberíamos encontrar la información en forma rápida sin importar la cantidad de elementos que tengamos en la estructura.
Un Hash no es más que un arreglo, en el cual podemos usar dos técnicas de ordenamiento interno. Este ordenamiento define donde colocar un elemento al insertar, pudiendo utilizarse dispersion abierta o dispersión cerrada.
Supongamos que tenemos el siguiente Hash:
En principio no es mas que un arreglo, pero crearemos un puntero en cada celda, de forma que podamos tener cualquier tipo de información guardad dentro de las mismas.
typedef struct tablahash{
int totalDisp;
nodoHash* hash[LARGOHASH+1];
};
Dijimos que el hash nos permite acceder en forma rápida a una de las posiciones dentro del mismo, esto se realiza mediante una función de dispersión que dada cierta entrada o valor, nos devuelve el valor dentro del hash donde debemos buscar la información que nos interesa.
Por ejemplo, si tenemos la lista de personas ingresadas por cédula, y le pasamos el numero de cédula 123456789 la función de dispersión nos devolverá la posición X dentro del hash donde debemos buscar la información de esa persona. Una función de dispersión básica pero útil suele ser sumar los valores ASCII de los caracteres y obtener el resto de dividir entre el largo del Hash, ya que no podemos obtener posiciones fuera del Hash mismo.
Un ejemplo de funcìón de dispersión sería el siguiente:
int calcularClaveInsertar(char const* id) {
int i, disp, length;
disp = 0;
length = strlen(id);for(i=0; i<length; i++)
disp += id[i];
disp = disp % LARGOHASH;return disp;
}
Esta función recibe un string y nos devuelve la posición correspondiente al mismo dentro del Hash de largo LARGOHASH.
Ya se habran dado cuenta que podemos tener problemas, que pasa si para dos cédulas diferentes tenemos el mismo resultados de dispersión? Y que sucede si tenemos muchos elementos, más de las posiciones disponibles dentro del hash? Estos casos son llamados «colisiones» ya que la información intenta ocupar el mismo lugar de memoria o posición dentro del hash. Para estos casos es que tenemos que analizar los dos tipos de dispersión posible, abierta y cerrada.
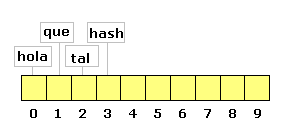
En el caso de la dispersión abierta lo que haremos al tener una colisión será simplemente tener una lista encadenada en cada nodo, por lo que iremos ampliando la lista a medida que tenemos colisiones. Si por ejemplo tenemo el hash de largo 10, e insertamos las cadenas «hola» (104+111+108+97 % 10 = 0), «que» (113+117+101 % 10 = 1), «tal» (116+97+108 % 10 = 1), «hash» (104+97+115+104 % 10 = 0) tendríamos un resultado como el siguiente:
En las posiciones 0 y 1 tuvimos colisiones por lo que tenemos dos listas de dos elementos en cada una. Estos nos lleva a ver que en el peor caso de un hash de dispersión abierta tendremos una única lista de elementos en una sola posición, con lo que nuestro hash será simplemente una lista y no nos será de mucha utilidad.
Por esta razón debemos tomar algunas precauciones al utilizar esta estructura de datos, debemos utilizar una función de dispersión adecuada, es decir que nos devuelva valores lo más distribuidos posibles, debemos utilizar un tamaño de hash mayor a la cantidad de elementos que tendremos o que suponemos llegaremos a tener, y es una buena práctica utilizar un número primo en el largo del hash de forma que nos tengamos muchas colisiones al dividir sobre el largo del hash.
El segundo caso, la dispersión cerrada, no permite la creación de listas, pudiendo haber un solo elemento por cada nodo del hash. Para resolver las colisiones se utilizan funciones de redispersión que permiten buscar otra posición dipsonible para el elemento.
Para las funciones de redispersión tenemos la posibilidad de realizar una función lineal, que al encontrar una colisión sume 1 a la posición encontrada, tratando de encontrar una celda libre a continuación. Por ejemplo si tuviéramos el caso anterior, lo que haríamos hubiera sido insertar la palabra «hola» en la posición 0, luego «que» en la posición 1, cuando vamos a insertar «tal» nos encontramos con la posición 1 ya ocupada, por lo que sumamos 1 y lo insertamos en la posición 2. Cuando vamos a insertar «hash» encontramos la posición 0 ocupada, pasamos a la 1 y lo mismo, sumamos 1 nuevamente y la 2 también esta ocupada por lo que pasamos a la 3 que sí esta libre e insertamos ahí.
Cuando vamos a buscar un elemento al hash caculamos la función de dispersión, por ejemplo para la palabra «tal», obtenemos el valor 1, vamos a esa posición y no lo encontramos. Entonces vamos sumando 1 hasta encontrarlo o que la celda sea vacía.
El problema sucede cuando eliminamos un elemento y «cortamos» esta cadena, de forma que no podemos seguir este procedimiento. Por ejemplo supongamos que eliminamos la palabra «tal», luego queremos saber si «hash» pertenece, para lo cual calculamos la dispersión, obtenemos 0, comenzamos a avanzar sumando 1, pasamos a la posición 1, luego a la 2 y llegamos a una celda vacía. No podemos saber que «hash» está en la próxima posición, ya que la celda vacía indica que se termino la cadena. Podríamos buscar una solución alternativa, por ejemplo marcar las casillas cuando borramos con un valor especial de forma que cuando buscamos y encontramos una de estas casillas sigamos avanzando sin detenernos. Así pasaríamos de la posición 2 a la 3 y econtraríamos «hash».
El problema con la dispersión cerrada lineal es que comenzamos a agrupar los elementos, de forma que terminamos nuevamente con una lista continua dentro del hash y terminamos trabajando como si se tratara de una lista, perdiendo la eficiencia de acceso rápido en el caso promedio.
Tenemos la posibilidad de modificar la función de redispersión, pasando de una lineal a una cuadrática, la cual nos permite dar «saltos» dentro del hash cuando tenemos colisiones. En lugar de sumar 1 al encontrar una colisión sumamos i^2, de esta forma sumamos 0, 1, 4, 9… evitando crear secuencias continuas en un principio. El problema en el caso de la redispersión cuadrática y de que el tamaño del hash es limitado, es que volvemos a caer sobre las mismas posiciones luego de varios saltos, por lo que no utilizamos todo el espacio disponible.
Con la redispersión cuadrática podemos utilizar hasta la mitad del tamaño del hash (si el largo del mismo es de tamaño primo). Es importante realizar un conteo de los elementos y en caso de que el hash este siendo llenado debemos realizar una reestructuración del hash, creando uno nuevo de mayor tamaño primo, por ejemplo un primo cercano al doble, e insertando los elementos del hash anterior en este nuevo hash. Esta operación es bastante costosa, aunque si se tiene cuidado en la elección del tamaño del hash según las características del problema no debería ser una operación frecuente.
Vemos un ejemplo del código de un hash con dispersión abierta. Definimos la estructura de datos como un arreglo con punteros:
// Nodo de un elemento en el hash
typedef struct nodoEtq {
char* idDisposivo;
nodoEtq* sig;
};// Nodo del hash
typedef struct nodoHash {
nodoEtq* disp;
};typedef struct tablahash {
int totalDisp;
nodoHash* hash[LARGOHASH+1];
};
Necesitaremos inicializar el hash, ya que las posiciones del arreglo son punteros.
// Inicializa todas las posiciones del hash
void inicializarHash (nodoHash** hash) {
int i;for (i = 0; i <= LARGOHASH; i++)
hash[i] = NULL;return;
}tablahash * hash = new tablahash;
inicializarHash(hash->hash);
hash->totalDisp = 0;
Luego necesitaremos la función de dispersión y una función auxiliar para saber si una celda del hash es vacía:
// Calcula la clave a usar para insertar
int calcularClaveInsertar(char const* id) {
int i, disp, length;
disp = 0;
length = strlen(id);for(i=0; i<length; i++)
disp += id[i];disp = disp % LARGOHASH;
return disp;
}// Celda vacia del hash
bool esVaciaCeldaHash(nodoHash** hash, int disp) {
return hash[disp] == NULL;
}
La función para insertar elementos en el Hash:
// Inserta en el hash un identificador
nodoEtq* insertarHash(nodoHash** hash, char* id) {
int disp;
nodoEtq* nodoEtiqueta = new nodoEtq;
nodoHash* nodoH = new nodoHash;
char* idDisp = new char[strlen(id)+1];nodoEtiqueta->idDisposivo = idDisp;
strcpy(nodoEtiqueta->idDisposivo,id);disp = calcularClaveInsertar(id);
if (hash[disp] == NULL) {
nodoEtiqueta->sig = NULL;
} else {
nodoEtiqueta->sig = hash[disp]->disp;
}nodoH->disp = nodoEtiqueta;
hash[disp] = nodoH;return nodoEtiqueta;
}// Inovación a la insersión
// Creamos un nuevo nodo, insertamos el char* idD e incrementamos la cantidad de elementos.
nodoEtq* nuevoNodo = new nodoEtq;
nuevoNodo = insertarHash(hash->hash, idD);
gl->totalDisp++;
Como dijimos al comenzar, la idea del hash es buscar elementos dentro del mismo en forma rápida, vemos una función para realizar las búsquedas:
// Indica si pertenece un identificador al hash
nodoEtq* perteneceHash(nodoHash** hash, char const* id) {
nodoEtq* nodo;
int pos;pos = calcularClaveInsertar(id);
if (esVaciaCeldaHash(hash, pos)) {
return NULL;
} else {
nodo = hash[pos]->disp;
while ((nodo != NULL) && (strcmp(nodo->idDisposivo,id) != 0)) {
nodo = nodo->sig;
}if (nodo != NULL) {
return nodo;
} else {
return NULL;
}}
}
Al utilizar dispersión abierta tenemos una lista en cada celda, por lo que luego de calcular la dispersión debemos recorrer la lista de ese nodo en busca del elemento o el fin de lista. En caso de encontrar el nodo lo devolvemos, o en caso contrario devolvemos NULL.
Por último, una función para desplegar el hash, puede ser útil para realizar pruebas o ver el estado del hash en un momento dado:
// Función auxiliar para desplegar la lista de cada nodo
void desplegarHashLista(nodoHash* lista) {
nodoHash* recorrer;recorrer = lista;
while (recorrer->disp != NULL) {
printf(«Valor: %s,», recorrer->disp->idDisposivo);
recorrer->disp = recorrer->disp->sig;
}return;
}// Despliega el hash
void desplegarHash (nodoHash** hash) {
int i;for (i = 0; i < LARGOHASH; i++) {
if (hash[i] == NULL) {
printf(«NULL «);
} else {
desplegarHashLista(hash[i]);
}
}return;
}
